常见排序算法

11 August 2021 - 3 mins read time
Tags: 基础知识学习

1 冒泡排序

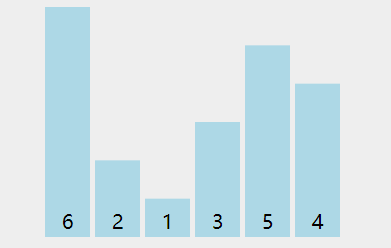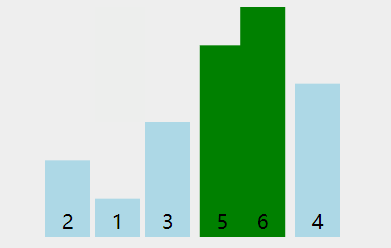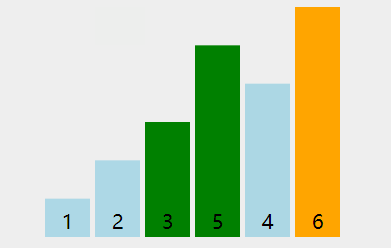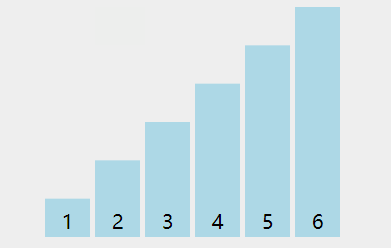
双重循环遍历数组，两两比较，并将最大值/最小值交换到最后一位

时间复杂度：\(O(n^{2})\)

空间复杂度：\(O(1)\)

class bubbleSort : public mySort {
public:
	vector<int> callSort(vector<int> nums) {
		cout << "Calling bubbleSort" << endl;
		int n = nums.size();
		for (int i = 0; i < n - 1; i++) {
			for (int j = 0; j < n - 1 - i; j++) {
				if (nums[j] > nums[j + 1]) {
					swap(nums[j], nums[j + 1]);
				}
			}
		}
		return nums;
	}
};

class bubbleSort_v2 : public mySort {
public:
	vector<int> callSort(vector<int> nums) {
		cout << "Calling bubbleSort_v2" << endl;
		int n = nums.size();
		bool swapped = true;
		for (int i = 0; i < n - 1; i++) {
			if (!swapped) {  // 如果某轮没发生任何交换，说明就已经是有序的了
				break;
			}
			swapped = false;
			for (int j = 0; j < n - 1; j++) {
				if (nums[j] > nums[j + 1]) {
					swap(nums[j], nums[j + 1]);
					swapped = true;
				}
			}
		}
		return nums;
	}
};

2 选择排序

双重循环遍历数组，每经过一轮比较，找到最小/最大元素的下标，将其交换之首位。

时间复杂度：\(O(n^{2})\)

空间复杂度：\(O(1)\)

class selectionSort : public mySort {
public:
	vector<int> callSort(vector<int> nums) {
		cout << "Calling selectionSort" << endl;
		int n = nums.size();
		for (int i = 0; i < n - 1; i++) {
			int minIdx = i;
			for (int j = i + 1; j < n; j++) {
				if (nums[j] < nums[minIdx]) {
					minIdx = j;
				}
			}
			swap(nums[i], nums[minIdx]);
		}
		return nums;
	}
};

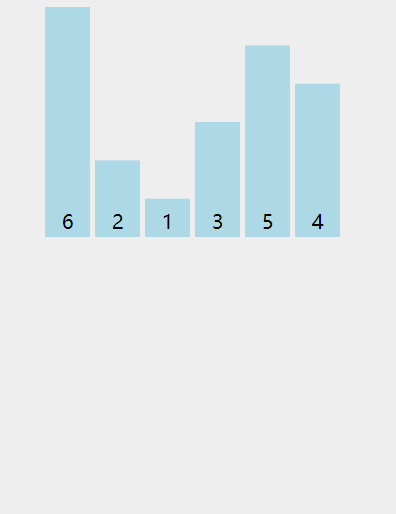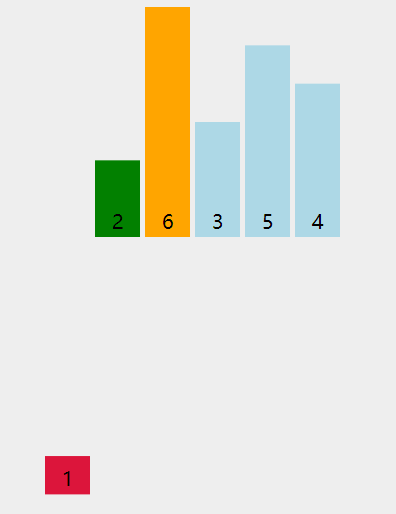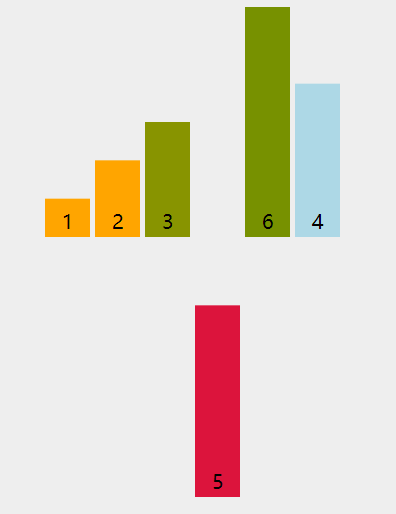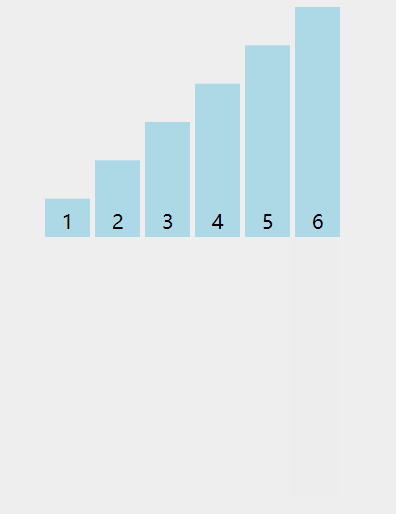
3 插入排序

在新数字插入过程中，不断与前面的数字比较，直到找到适合自己的位置。

时间复杂度：\(O(n^{2})\)

空间复杂度：\(O(1)\)

3.1 交换法

class insertSort : public mySort {
public:
	vector<int> callSort(vector<int> nums) {
		cout << "Calling insertSort" << endl;
		int n = nums.size();
		for (int i = 1; i < n; i++) {
			int j = i;
			while (j >= 1 && nums[j] < nums[j - 1]) {
				swap(nums[j], nums[j - 1]);
				j--;
			}
		}
		return nums;
	}
};

3.2 移动法

class insertSort_v2 : public mySort {
public:
	vector<int> callSort(vector<int> nums) {
		cout << "Calling insertSort_v2" << endl;
		int n = nums.size();
		for (int i = 1; i < n; i++) {
			int currentNum = nums[i];
			int j = i - 1;
			while (j >= 0 && currentNum < nums[j]) {
				nums[j + 1] = nums[j];
				j--;
			}
			nums[j + 1] = currentNum;
		}
		return nums;
	}
};

快速排序

基本思想： Step1: 从数组中取一个数，称之为基数(pivot)，通常取第一个元素； Step2: 遍历数组，将比基数大的数字放到它的左边，比基数小的数字放到它的右边。遍历完成后，数组被分为左右两个区域； Step3: 将左右两个区域视为两个数组，重复前两个步骤，直到排序完成。

时间复杂度：\(O(nlogn)\) 空间复杂度：\(O(logn)\)

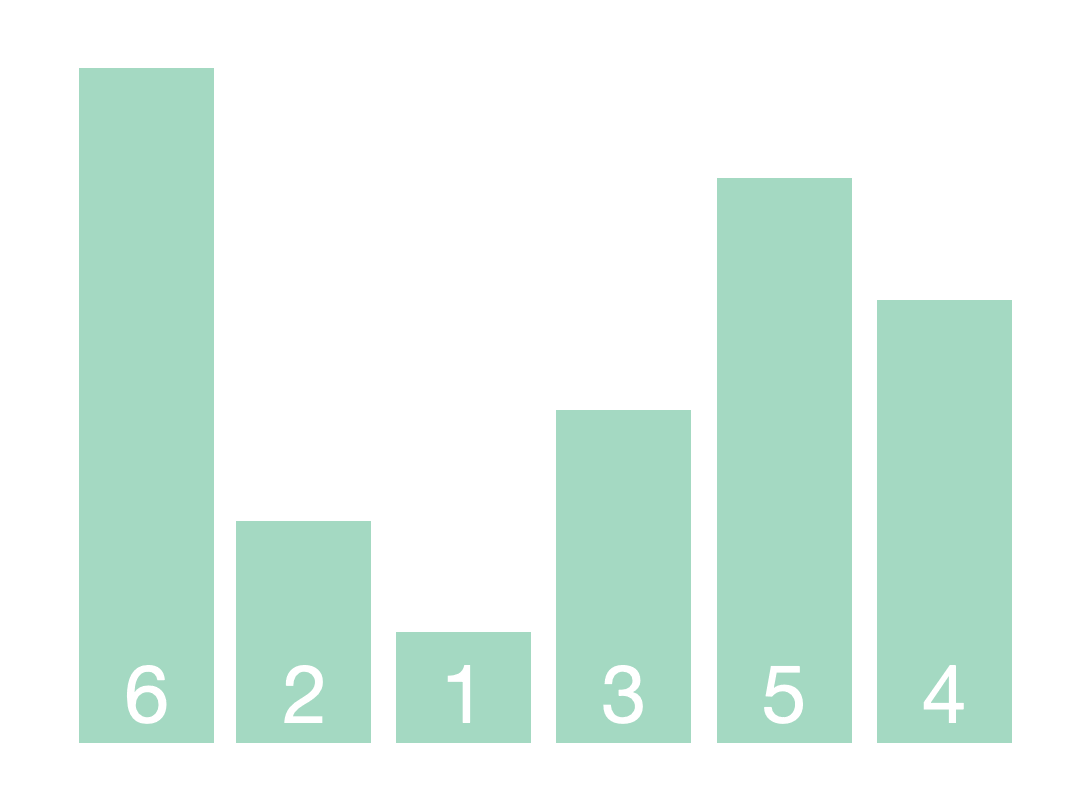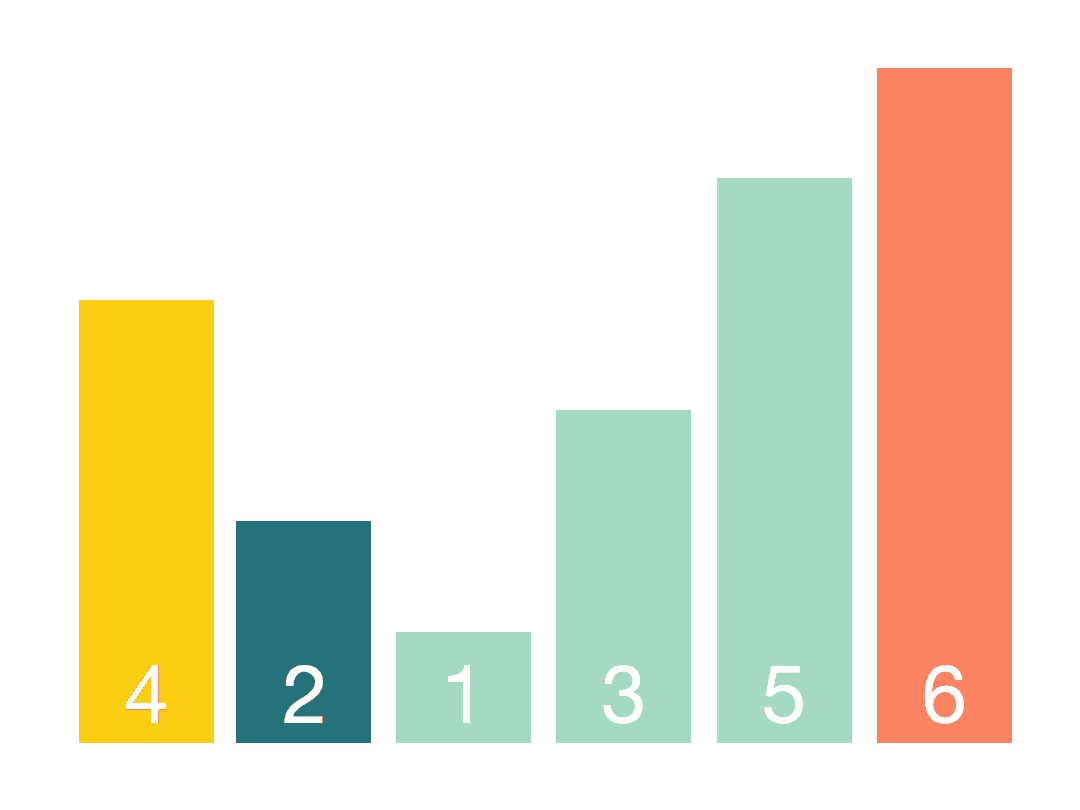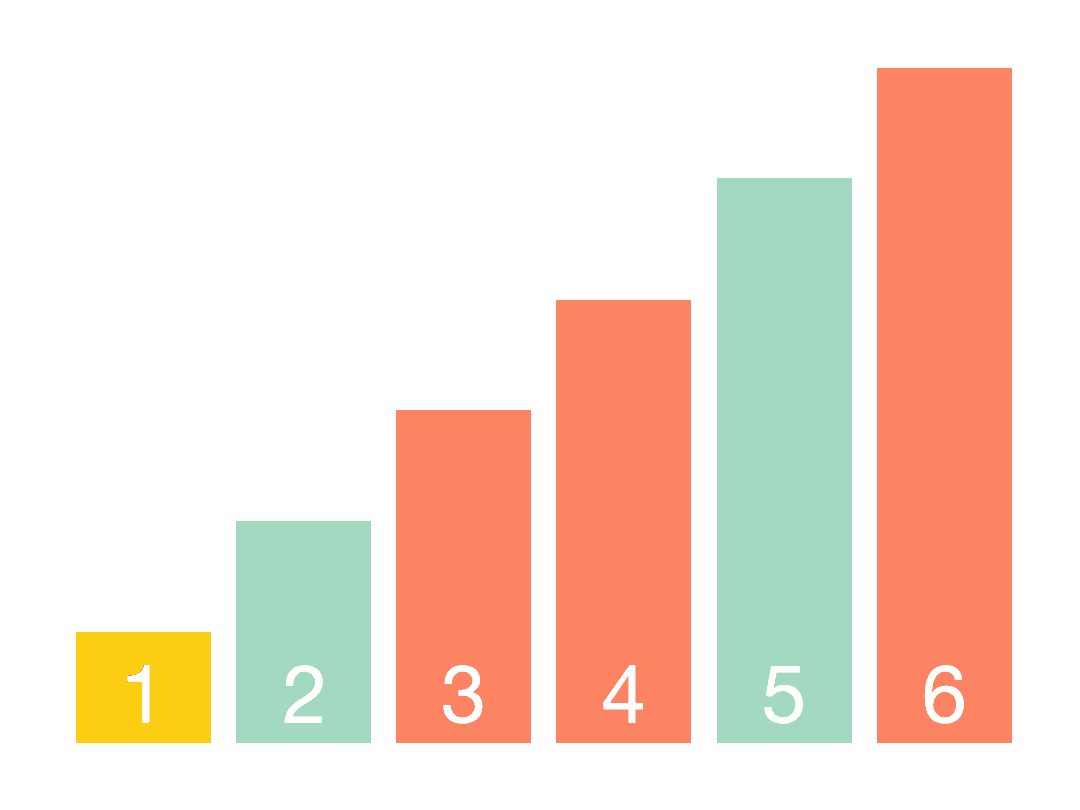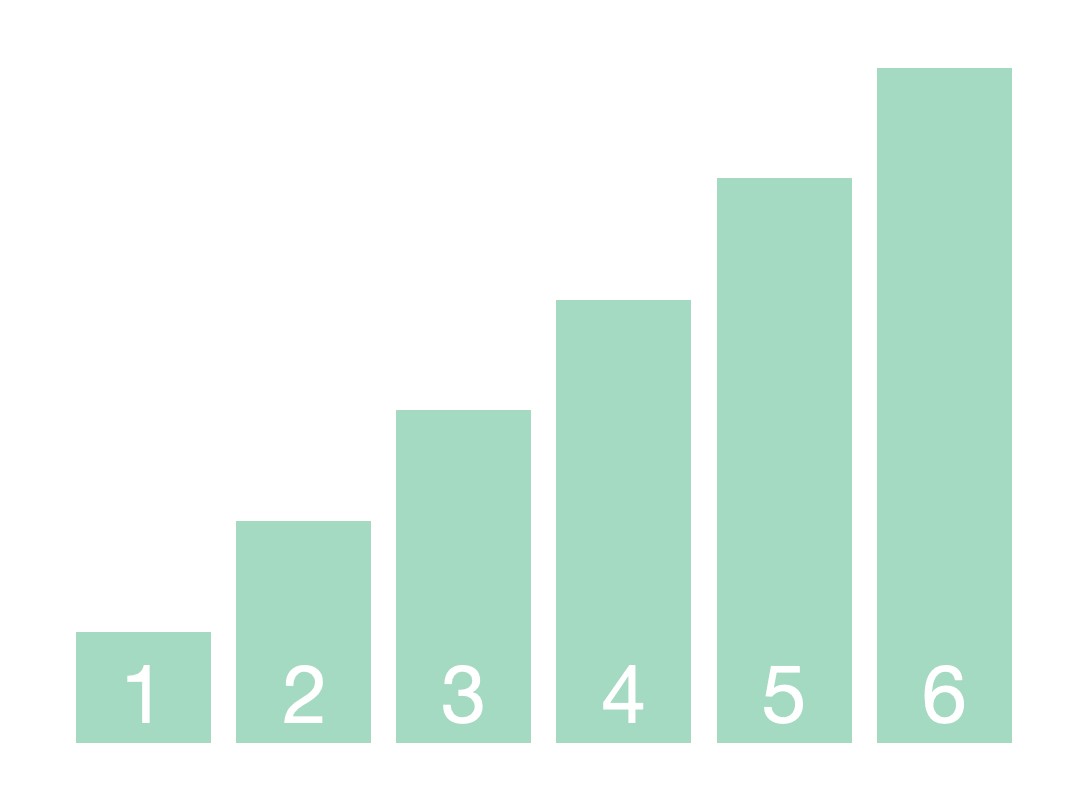
class quickSort : public mySort {
public:
	vector<int> callSort(vector<int> nums) {
		cout << "Calling quick sort" << endl;
		quick_sort(nums);
		return nums;
	}
	void quick_sort(vector<int>& arr) {
		int n = arr.size();
		quick_sort(arr, 0, n - 1);
	}

	void quick_sort(vector<int>& arr, int start, int end) {
		// 若区域内的数字少于两个，退出递归
		if (start >= end) return;

		// 将数组分区，获取中间值的下标
		int middle = partition(arr, start, end);

		// 对左边区域进行快排
		quick_sort(arr, start, middle - 1);

		// 对右边区域进行快排
		quick_sort(arr, middle + 1, end);
	}

	// 将arr从start到end进行分区，左边区域比基数小，右边区域比基数大，然后返回中间值的下标
	int partition(vector<int>& arr, int start, int end) {
		// 取第一个数为基数
		int pivot = arr[start];
		// 从第二个数开始分区
		int left = start + 1;
		int right = end;

		while (left < right) {
			// 找到第一个大于基数的位置
			while (left < right && arr[left] <= pivot) {
				left++;
			}
			if (left != right) {
				swap(arr[left], arr[right]);
				right--;
			}
		}

		if (left == right && arr[right] > pivot) {
			right--;
		}

		if (right != start) {
			swap(arr[right], arr[start]);
		}
		return right;
	}
};