几种常见的激活函数

05 July 2020 - 2 mins read time
Tags: 深度学习相关

激活函数在神经网络中起到了重要的作用，如果没有激活函数，层数再多的网络也只是线性模型，很可能无法正确地对复杂模式进行学习。

激活函数作用于每一层节点的输出之后，通过引入激活函数，网络具有了非线性关系的能力，从而获得更好的特征表达。接下来，介绍几种常见的激活函数：

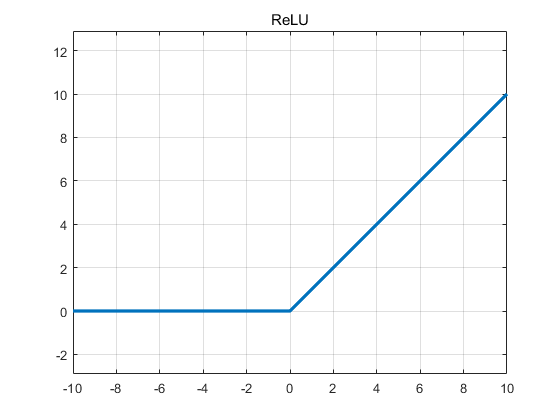
ReLU

def relu(x):
    return max(x, 0)
\[y= \begin{cases} x, x > 0 \\ 0, x \le 0 \end{cases}\]

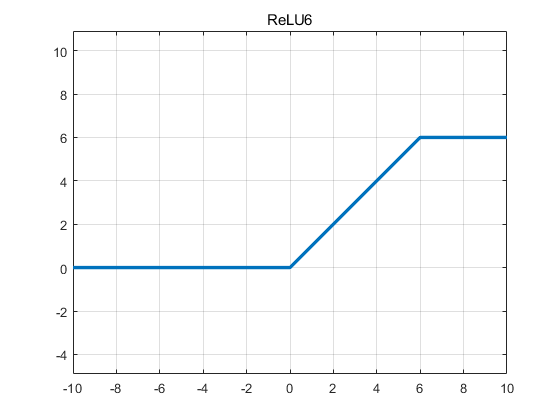
ReLU6

这里为什么是6，而不是其它数字，其实是经过实验验证得来的，取6通常可以得到最好的结果。

def relu6(x):
    return min(max(x, 0), 6)
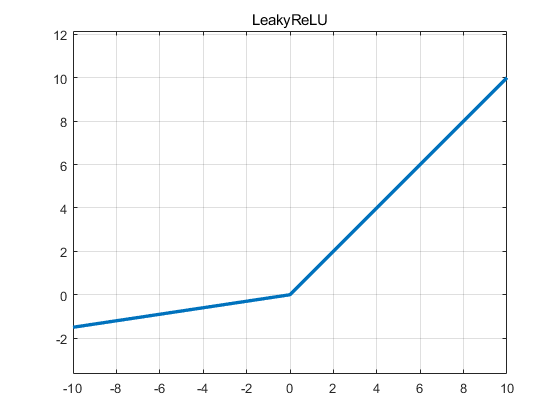
\[y= \begin{cases} 6, x > 6 \\ x, 0 < x \le 6 \\ 0, x \le 0 \\ \end{cases}\]

LeakyReLU

def leakyRelu(x, a):
    # variable 'a' is a fixed coefficient 
    return max(x, a * x)

# more efficient implementation
def leakyRelu(x, a, name="lrelu"):
     with tf.variable_scope(name):
         f1 = 0.5 * (1 + a)
         f2 = 0.5 * (1 - a)
         return f1 * x + f2 * abs(x)
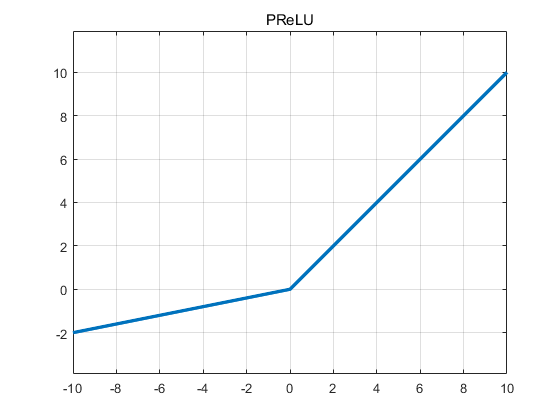
\[y= \begin{cases} x, x > 0 \\ ax, x \le 0\ and\ a\ is\ fixed \end{cases}\]

PReLU

相较于LeakyReLU,PReLU的系数是可以变化的，出自这篇文章Delving Deep into Rectifiers : Surpassing Human-Level Performance on ImageNet Classification，回头看看。

def prelu(_x, name):
    # variable 'a' is learnable
    _alpha = tf.get_variable(name + "prelu",
                             shape=_x.get_shape()[-1],
                             dtype=_x.dtype,
                             initializer=tf.constant_initializer(0.1))
    pos = tf.nn.relu(_x)
    neg = _alpha * (_x - tf.abs(_x)) * 0.5

    return pos + neg
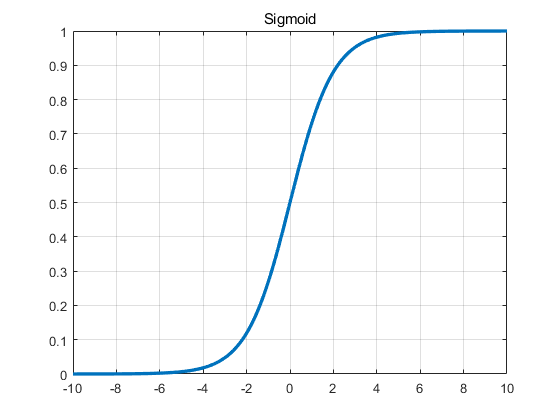
\[y= \begin{cases} x, x > 0 \\ ax, x \le 0\ and\ a\ is\ learnable \end{cases}\]

Sigmoid

def sigmoid(x):
    return 1 / (1 + np.exp(-x))
\[y= \frac{1}{1+e^{-x}}\]

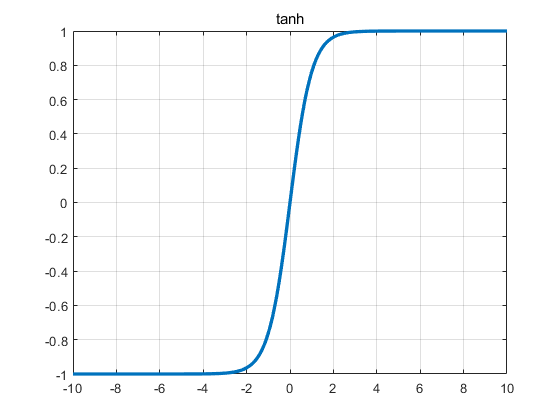
tanh

def tanh(x):
    return (1 - np.exp(-2 * x)) / (1 + np.exp(-2 * x))
\[y= \frac{1 - e^{-2x}}{1 + e^{-2x}}\]